superficie laterale
|
superficie totale
|
volume
| |
|---|---|---|---|
| piramide qualsiasi | |||
| piramide retta | |||
| tronco di piramide |  |
Piramide
La piramide è un poliedro limitato da un poligono qualsiasi e da tanti triangoli quanti sono i lati di questo poligono, aventi tutti un vertice in comune. | |
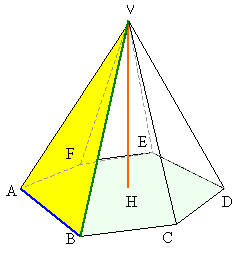 |
LEGENDA
V verticeABCDEF base (poligono di base) VAB faccia laterale (triangolo) VH altezza (distanza tra il vertice e la base) VM apotema H piede dell’altezza VB spigolo laterale AB spigolo di base |
| Una piramide si dice retta se il poligono di base è circoscrittibile a una circonferenza e il piede dell’altezza coincide con il centro di questa circonferenza. L’apotema di una piramide retta è l’altezza di una delle sue facce. Una piramide si dice regolare se è retta ed il poligono di base è un poligono regolare. | 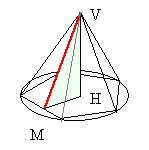 |
Tronco di piramide
Tagliando una piramide con un piano parallelo alla base si ottengono due solidi: uno è ancora una piramide , l’altro è un tronco di piramide. I due poligoni che lo delimitano costituiscono le basi del tronco di piramide, e le facce laterali sono dei trapezi. La distanza tra le basi è l’altezza del solido.Un tronco di piramide si dice retto se è stato ottenuto da una piramide retta. Un tronco di piramide si dice regolare se è stato ottenuto da una piramide regolare. Le facce laterali di un tronco di piramide regolare sono tutti trapezi isosceli congruenti. L’altezza di uno qualsiasi di questi trapezi è l’apotema del tronco di piramide. | 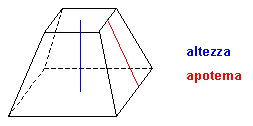 |

0 commenti :
Posta un commento